Comparison of estimatorsAbstract
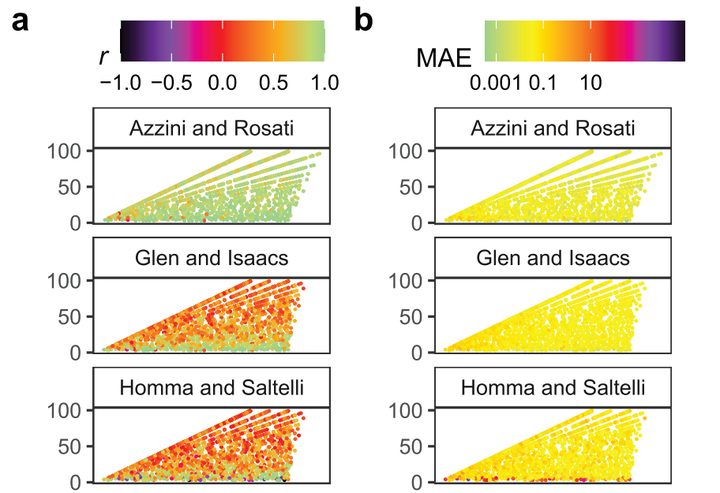
Sensitivity analysis helps identify which model inputs convey the most uncertainty to the model output. One of the most authoritative measures in global sensitivity analysis is the Sobol' total-order index, which can be computed with several different estimators. Although previous comparisons exist, it is hard to know which estimator performs best since the results are contingent on the benchmark setting defined by the analyst (the sampling method, the distribution of the model inputs, the number of model runs, the test function or model and its dimensionality, the weight of higher order effects, or the performance measure selected). Here we compare several total-order estimators in an eight-dimension hypercube, where these benchmark parameters are treated as random parameters. This arrangement significantly relaxes the dependency of the results on the benchmark design. We observe that the most accurate estimators are from Razavi and Gupta, Jansen, or Janon/Monod for factor prioritization, and from Jansen, Janon/Monod, or Azzini and Rosatifor approaching the “true” total-order indices. The rest lag considerably behind. Our work helps analysts navigate myriad total-order formulae by reducing the uncertainty in the selection of the most appropriate estimator.
William Becker
I am a freelance data scientist working at the intersection between data, research and policy. I work for many international organisations, including the European Commission, and various UN agencies, with a particular specialisation in building (composite) indicator solutions. I am also a researcher in various fields, including sensitivity analysis.
Samuele Lo Piano
From Dec 1 2019 I am working in the CREDS research centre (Centre for Research into Energy Demand Solutions), flexibility theme area. My research interests include energy systems, sensitivity auditing, uncertainty quantification and global sensitivity analysis, science for governance, modelling and model (knowledge) quality assessment. My research interests also cover complexity and complex systems (such as societies).
Andrea Saltelli
Works on Sensitivity analysis, sensitivity auditing, impact assessment, science integrity, sociology of quantification, science and lobbies, science and post truth….